Now that we have expressed the computation in this language, we need to “unroll” it, by writing it as a sequence of lines, all of them following this format:
var_x1 = (C1 * var_01 + C2 * var_02 + … + Cn * var_n) * (D1 * var_01 + D2 * var_02 + … + Dn * var_n)
Each of these lines is called a “gate”; that’s because this unrolled computation can be seen as a digital circuit, where the left side of the equation (var_x1) is the output of the “multiplication gate” that takes as inputs the two factors being multiplied: (C1 * var_01 + C2 * var_02 + … + Cn * var_n) and (D1 * var_01 + D2 * var_02 + … + Dn * var_n). Actually, all the computation in this “unrolled” format is somehow similar to a board for electronic circuits, that just supports wiring, and sequences of sums and multiplication of signals; in this model variables are, at each step, the inputs and outputs of the next set of multiplication “gates”, with the same signal that can be input to many different gates. That’s why you’ll see the terms “circuit” and “gates” used a lot in zero-knowledge texts; and in the code too: in libsnark, the main and original zk-Snark C++ library, the computation is coded over an object named “protoboard” .
Anyway, we were saying that each line of the computation is just a multiplication of sums of variables, and that its result is assigned to another variable. This step will typically require the introduction of many new variables that store the intermediate steps of the computation. As we’ve seen before, we’ll use all possible tricks to express complex computations as just sums and multiplications over a finite field. This will typically require mapping of the numeric types used, e.g. floating point numbers could be expressed as fraction and exponent, and in turn fraction and exponent could be mapped to their bit representation, one variable for each bit. It’s all doable, and we know it is because we are mapping today complex math on our computers, that are indeed digital circuits; the only problem is that the number of variables and lines can become rapidly huge, and that can quickly become a problem. If, however, our computation is just made of simple arithmetic on integer numbers, it’s all very easy, and our original example:
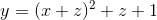
y = (x+z)^2 + z +1
can now be expressed in our new format as:
